【双曲线渐进方程】双曲线的渐进线为什么是把1换成0?
中学生都知道双曲线,就算现在不知道,用不了多久也会知道。我相信大家学到这一点的时候,第一个想到的就是这里的双曲线和我们反比例函数的双曲线之间的关系,关于这一点,请参看拙文《双曲线与反比例函数》,里面有详细的介绍。今天要谈得,是关于双曲线的渐近线,为什么双曲线的渐近线就是把1换成0?首先对于什么是渐近线我想就不用我说,考虑圆锥曲线:
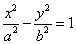
我们知道,其渐近线方程为y=±b/ax,如果你容易记错,那么很简单,你只需把双曲线方程右边的1换成零,就是双曲线的渐近线方程了
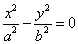
我们不禁要问,为什么这么神奇?为什么把1换成零就是渐近线方程?这个原理有什么直观上的含义么?虽然我们完全可以证明这个方法的合理性,但是我想每一位同学都很想从直观的角度来看,看这里面究竟隐藏着什么?!今天,我们就用极限的观点来看这个有趣的问题(画图像花了半天,所以这么晚才发表啊!)
现在考虑这样的一个双曲线族。就是一系列双曲线
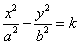
其中k为常数,不同的k值对应着不同的双曲线,我想大家可以看出来,这样画出来的所有双曲线都有相同的渐近线。为了方便,我们画出当k=1、0.36、0.1、0.01时候的双曲线:
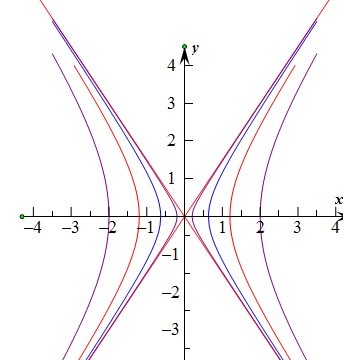
最外面的双曲线是k=1,其次是k=0.36,k=0.1,k=0.01时候的双曲线,我们不禁发现,当k越来越小,函数的图像就越来越靠近渐近线!可以看到当k=0.01的时候,双曲线已经基本上和渐近线重合了,如果k取更小的值得话,画出来的图像就更加接近于渐近线。所以,k=0时候的函数图像就是这一系列双曲线的极限状态。这就是为什么我们求双曲线的渐近线的时候,只需把右边的1换成零。
文章来源:学夫子数学博客





